“In the early morning hours of June 1, 2009, Air France Flight AF 447, with 228 passengers and crew aboard, disappeared during stormy weather over the Atlantic while on a flight from Rio de Janeiro to Paris.” So begin Lawrence Stone and colleagues from Metron Scientific Solutions in Reston, Virginia, in describing their role in the discovery of the wreckage almost two years after the loss of the aircraft.

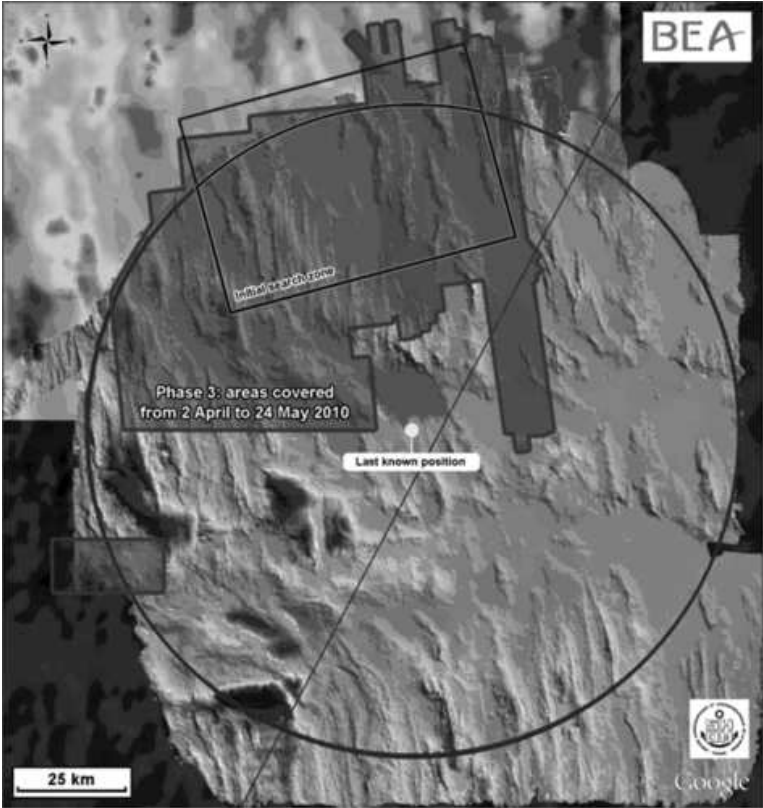
Stone and co are statisticians who were brought in to reëxamine the evidence after four intensive searches had failed to find the aircraft. What’s interesting about this story is that their analysis pointed to a location not far from the last known position, in an area that had almost certainly been searched soon after the disaster. The wreckage was found almost exactly where they predicted at a depth of 14,000 feet after only one week’s additional search.

Today, Stone and co explain how they did it. Their approach was to use a technique known as Bayesian inference which takes into account all the prior information known about the crash location as well as the evidence from the unsuccessful search efforts. The result is a probability distribution for the location of the wreckage.

Bayesian inference is a statistical technique that mathematicians use to determine some underlying probability distribution based on an observed distribution. In particular, statisticians use this technique to update the probability of a particular hypothesis as they gather additional evidence.

In the case of Air France Flight 447, the underlying distribution was the probability of finding the wreckage at a given location. That depended on a number of factors such as the last GPS location transmitted by the plane, how far the aircraft might have traveled after that and also the location of dead bodies found on the surface once their rate of drift in the water had been taken into account.

All of this is what statisticians call the “prior.” It gives a certain probability distribution for the location of the wreckage.

However, a number of searches that relied on this information had failed to find the wreckage. So the question that Stone and co had to answer was how this evidence should be used to modify the probability distribution.

This is what statisticians call the posterior distribution. To calculate it, Stone and co had to take into account the failure of four different searches after the plane went down. The first was the failure to find debris or bodies for six days after the plane went missing in June 2009; then there was the failure of acoustic searches in July 2009 to detect the pings from underwater locator beacons on the flight data recorder and cockpit voice recorder; next, another search in August 2009 failed to find anything using side-scanning sonar; and finally, there was another unsuccessful search using side-scanning sonar in April and May 2010.

The searches all took place in different, sometimes overlapping areas, within 40 nautical miles of the last known location of the plane. These areas were calculated on the basis of how far debris and bodies were thought to have drifted due to wind and currents. And the search that listened for the acoustic pings from the aircraft’s data recorders almost certainly covered the location where the wreckage was eventually found.

That’s an important point. A different analysis might have excluded this location on the basis that it had already been covered. But Stone and co chose to include the possibility that the acoustic beacons may have failed, a crucial decision that led directly to the discovery of the wreckage. Indeed, it seems likely that the beacons did fail and that this was the main reason why the search took so long.

The key point, of course, is that Bayesian inference by itself can’t solve these problems. Instead, statisticians themselves play a crucial role in evaluating the evidence, deciding what it means and then incorporating it in an appropriate way into the Bayesian model.

The end result, in this case at least, was the discovery of the wreckage along with the flight data recorder and cockpit voice recorder, which provided vital evidence about the aircraft’s final moments (although there are still some dispute about exactly what caused the disaster). It also led to the discovery of many more bodies that were then reunited with grieving families.

This story of the statistical search for a missing aircraft is hugely relevant now because of the ongoing search for Malaysia Airlines flight MH 370 which disappeared en route from Kuala Lumpur to Beijing on March 8. Nothing has been seen or heard from it again.

The lesson from the search for Air France flight AF 447 is that Bayesian inference is a powerful tool in searches of this kind but that the way it is applied is crucial too. In other words, statisticians are going to have to play an important role in this search too.

Let’s hope that the assumptions used to update future searches for MH 370 are ultimately as successful as those that Stone and co employed in 2011.

Ref: arxiv.org/abs/1405.4720 : Search for the Wreckage of Air France Flight AF 447