Information Theory Reveals Size of Whale and Dolphin Communication Repertoires
One of the great unsung heroes of 20th-century physics is Claude Shannon who more or less single-handedly invented information theory in the 1940s. Shannon used his theory to work out the fundamental limits of how much we can compress data as well as how reliably we can store and send it.
Shannon immediately began to use his theory to study the information content of the English language. One approach was to use volunteers to guess the missing letters in words to work out their information content. From this his study of the size and number of frequently used words, Shannon was able to gauge the complexity of human language.
Today, Reginald Smith, an independent researcher at the Citizen Scientists League in Rochester, New York, suggests an interesting new way to analyse animal communication. His approach is to take Shannon’s approach in reverse– to start with a measure of the complexity of the language and use that to work out the size and number of the different “words” it contains. The result is an interesting estimate of the repertoires that different animals use to communicate.
Back in the 1940s, Shannon revolutionised the study of information. In particular, he looked at conditional entropy, the amount of information that a single letter conveys when it follows another letter or sequence of letters.
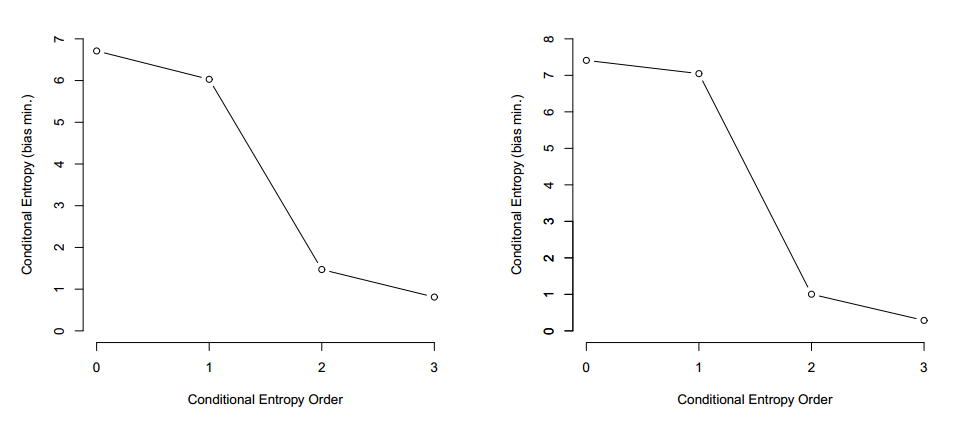
For the English alphabet of 26 letters plus the space character, Shannon calculated that a single letter conveys just over four bits of information when it follows another single letter. For a letter following a two-letter sequence, the entropy is 3.56 bits and for a letter following a 3-letter sequence, it is 3.3 bits. These values are known as the first, second and third order entropies.
That discovery had a profound effect on biologists who were hugely curious about the information content of animal communication. Since then, many groups have recorded various types of animal communication and calculated its information content.
The results clearly show that animal communication involves significant amounts of information. For example, the information entropy of bee dances is 2.54 bits.
However, the complexity of animal communication is not so clear. In general, the complexity depends on the order of dependence. For example, many bird call sequences show a high information content for first-order dependence, but the information content drops significantly when it comes to the second and third order dependences.
That seems to suggest that the complexity of bird call communication is relatively low. However, Smith points out that the results are highly sensitive to the size of the bird repertoires. This is clearly a problem when there is only a small amount of experimental data to work with.
For example, if birds have a large repertoire of different 2-letter and 3-letter words, then a proper analysis requires a significantly larger sample of bird calls than if their repertoire is small.
So an important question is just how big these animal repertoires are.
Smith’s new insight is that there is another way to work out the size of the repertoire of various different word lengths. He points out that the first order entropy of a language is intimately linked to the exact number of possible word-length combinations.
So given a measure of the first order entropy of a language, it is possible to use this combinatorics method to work out the likely repertoire of different word lengths.
Smith uses this insight to re-examine the data gathered for several different types of animal, such as bottlenose dolphins, humpback whales and various types of starling, thrush and skylark. For each species, he calculates the maximum and minimum repertoire of 1-letter, 2-letter and 3-letter “syllables” that appear in the data.
The results make for interesting reading. Smith calculates that bottlenose dolphins have a repertoire of 27 single letter syllables, five 2-letter syllables and four or five 3-letter syllables. By contrast, humpback whales have a repertoire of only six single letter syllables but use seventeen or eighteen 2-letter syllables (the data is not extensive enough to reveal the repertoire of 3-letter syllables).
The birds seem to have much larger vocabularies. European starlings, for example, use over 100 single letter syllables but could use as many as 78 3-letter syllables or as few as 6.
Perhaps Smith’s most important finding is that the amount of information he is able to extract about the repertoires is seriously constrained by the size of the datasets and that more work is needed to expand them. “In the end, the best way to accurately measure the repertoire sizes, particularly for dolphins and humpback whales, is to make a much larger measurement of sequences,” he concludes.
That’s interesting work. While it cannot reveal the intent or possible meaning of these animal communications, it certainly reveals some of its complexity.
And Smith has high expectations for the future if more data can be gathered. “It is the author’s hope that information theory analyses can help peel back the layers of complexity to show how closely such animal communication matches—or is distinct from—human language”, he says.
Ref: arxiv.org/abs/1308.3616 : Complexity In Animal Communication: Estimating The Size Of N-Gram Structures
Keep Reading
Most Popular
Large language models can do jaw-dropping things. But nobody knows exactly why.
And that's a problem. Figuring it out is one of the biggest scientific puzzles of our time and a crucial step towards controlling more powerful future models.
How scientists traced a mysterious covid case back to six toilets
When wastewater surveillance turns into a hunt for a single infected individual, the ethics get tricky.
The problem with plug-in hybrids? Their drivers.
Plug-in hybrids are often sold as a transition to EVs, but new data from Europe shows we’re still underestimating the emissions they produce.
Stay connected
Get the latest updates from
MIT Technology Review
Discover special offers, top stories, upcoming events, and more.