A small-scale demonstration shows how quantum computing could revolutionize data analysis
Over the past few decades, topology—a branch of mathematics dealing with shapes that can be turned into other shapes by processes like bending and stretching—has evolved from an arcane pursuit into an increasingly powerful tool for analyzing the real world. The role of symmetry in the topological world has turned out to be particularly important.
A symmetry is any property that stays the same as the viewpoint changes. A square looks the same as it rotates through 90 degrees, for example. That form of invariance is called rotational symmetry.
But there are some topological structures that persist across scales. Mathematicians call these symmetries persistent homologies, and the study of them is turning out to be the key to a wide range of problems such as network analysis, data mining, and understanding the brain’s wiring diagram.
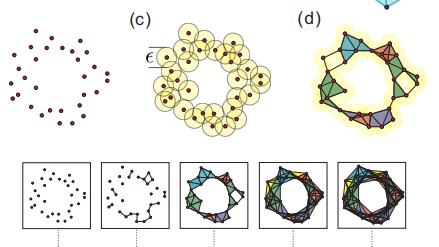
In theory, these symmetries are straightforward to characterize by counting, for example, the number of holes and voids in the structure of data. The resulting numbers are called Betti numbers, and structures with the same Betti numbers are topologically equivalent.
But there is a problem. Betti numbers are computationally demanding to calculate, “quickly overwhelming even the most powerful classical computers, even for not-so-large data sets,” say He-Liang Huang at the University of Science and Technology of China in Hefei and colleagues. Because of this, mathematicians have had limited success in exploiting the power of Betti numbers to study real-world problems.
Today, that looks set to change thanks to the work of Huang and co, who have calculated Betti numbers using a quantum computer for the first time. “Our experiment suggests that data analytics may be an important future application for quantum computing, with widespread applications in our increasingly data-centric world,” they say.
The demonstration builds on the work of MIT’s Seth Lloyd and colleagues, who in 2016 developed a quantum algorithm that could dramatically speed up the calculation of Betti numbers. On a conventional computer, this process scales with the number of data points as 2n. Lloyd and co’s quantum algorithm scales with n5—exponentially faster than the best known classical algorithm. But this research was entirely theoretical.
The work that Huang and co have done is to run this algorithm on a quantum computer in a proof-of-principle experiment. The team uses a six-photon quantum processor to analyze the topological features of Betti numbers in a network of three data points at two different scales. And the outcome is exactly as expected.
Of course, this example is not so hard for classical computers or even human brains to analyze. But the key point is that the Chinese have made it work on a quantum computer, a device that is set to dramatically outperform conventional computers in the coming years.
That sets the stage for an entirely new way to analyze the complex data sets that different scientific disciplines are increasingly producing. “Future advances in the field could open up new frontiers in data analysis for quantum computing, including signal and image analysis, astronomy, network and social media analysis, behavioral dynamics, biophysics, oncology and neuroscience,” say Huang and co.
So expect to hear more about Betti numbers and topological data analysis in the near future.
Ref: arxiv.org/abs/1801.06316 : Demonstration of Topological Data Analysis on a Quantum Processor
Deep Dive
Computing
Inside the hunt for new physics at the world’s largest particle collider
The Large Hadron Collider hasn’t seen any new particles since the discovery of the Higgs boson in 2012. Here’s what researchers are trying to do about it.
How ASML took over the chipmaking chessboard
MIT Technology Review sat down with outgoing CTO Martin van den Brink to talk about the company’s rise to dominance and the life and death of Moore’s Law.
How Wi-Fi sensing became usable tech
After a decade of obscurity, the technology is being used to track people’s movements.
Algorithms are everywhere
Three new books warn against turning into the person the algorithm thinks you are.
Stay connected
Get the latest updates from
MIT Technology Review
Discover special offers, top stories, upcoming events, and more.