Back in the 1880s, the American astronomer Simon Newcomb noticed something strange about the book of logarithmic tables in his library—the earlier pages were much more heavily thumbed than later ones implying that people looked up logarithms beginning with “1” much more often than “9.”

After some investigation, his concluded that in any list of data, numbers beginning with the digit “1” must be much more common than numbers beginning with other digits. He went on to formulate mathematical rationale behind this phenomenon, which later became known as Benford’s law, after the physicist Frank Benford who discovered it independently some 50 years later.

Benford’s law is highly counterintuitive. After all, it is not immediately clear why numbers beginning with “1” should be more common than others. Indeed, the law predicts that in data that conform to this rule, numbers with the first digit “1” should occur about 30 percent of the time while numbers beginning with the digit “9” should make up less than 5 percent of the total.

That turns out to be generally true for a wide range of data sets and, indeed, almost any data set that spans several orders of magnitude. That includes populations of towns, stock-market prices, physical constants, numbers in an issue of Reader’s Digest, and so on.

Although bizarre, Benford’s law turns out to be hugely useful for detecting financial fraud. The idea is that if people make up figures, the first digits in the data should be distributed fairly uniformly. Indeed, whenever there is an external influence over people’s behavior, the possibility arises of a deviation from Benford’s law.

Of course, a data set that deviates from Benford’s law is not proof of fraud, only an indication that further investigation is required.

But while statisticians have looked for Benford’s law in many data sets, they have never applied it to the world of social networks. Today that changes thanks to the work of Jennifer Golbeck at the University of Maryland in College Park. She shows that not only does Benford’s law apply to many data sets associated with social networks, but that deviations from this law are clearly linked to suspicious activity online.

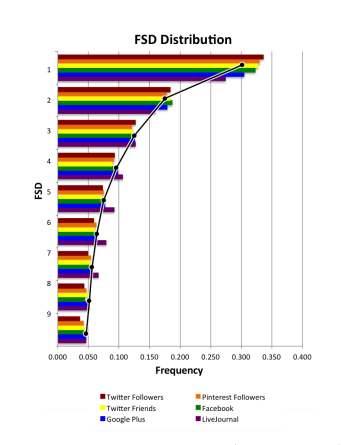
Golbeck begins with data on users from five major social networks: Facebook (18,000 users), Twitter (78,000 users), Google Plus (20,000 users), Pinterest (40 million users) and LiveJournal (45,000 users). Her method was straightforward. She looked at the number of friends and followers associated with each user in these data sets and counted the distribution of first digits in the figures.

The results make for interesting reading. In every data set, except one, the statistical distribution of first digits closely follows Benford’s law.

That’s not really a surprise. There is no reason why these data sets, which span several orders of magnitude, should not follow Benford’s law. But one dataset did not follow Benford’s law. This occurred in the number of follows on Pinterest. Golbeck points out that this by itself does not indicate fraudulent activity but certainly suggests that further investigation is required.

It didn’t take long for Golbeck to identify the cause. It turns out that when people join Pinterest, they are required to follow five or more “interests” before they can continue with the registration process. This creates at least five initial follows for each user. “Though users can go in and later delete those follows, few do, and this initiation process affects the entire distribution of FSDs,” she says.

That’s an interesting example of how an external influence causes a data set to deviate from Benford’s law. Forensic accountants look for similar deviations in financial data but these deviations are not always indicative of fraud. For example, the number 3 may crop up more often than expected in a company’s books if it frequently buys products costing £39.99.

Golbeck has gone further to see whether Benford’s law suggests suspicious activity on social networks. In particular, she looked not just at each individual’s number of friends but at the networks of their friends, so-called egocentric networks.

She then measured the correlation between an individual’s egocentric network and Benford’s law and found that for the vast majority of people, this correlation was greater than 0.9. “Overall, the vast majority of egocentric networks conformed to what Benford’s Law predicted,” she says.

In the case of Twitter, only 170 people out of the 21,000 that she investigated had a correlation lower than 0.5. Golbeck investigated each one of these with curious results.

“Almost every one of the 170 accounts appeared to be engaged in suspicious activity,” she says.

Some of the accounts were clearly spam but most were part of a network of Russian bots that post random snippets of literary works or quotations. “All the Russian accounts behaved the same way, following other accounts of their type, posting exactly one stock photo image, using a different stock photo image as the profile picture,” she says.

Just why these accounts exist, and for what purpose, is not clear. But their behavior is highly unusual. In fact, only two of the 170 accounts with a low correlation with Benford’s law seem to belong to legitimate users, says Golbeck.

That’s interesting work that has important implications for social network forensics. In recent years, it has become increasingly difficult to spot accounts on social networks that are engaged in suspicious activity. Comparing a large number of these against Benford’s law is a quick and simple way to find ones that require further investigation.

Of course, this process will not find all suspicious accounts. Any account that grows in the same way as a conventional one would remain hidden and it’s possible that maleficent users could employ simple techniques to make their accounts less identifiable now that this method has been revealed.

But for the time being, Benford’s law looks to be a valuable tool in the war against fraud and suspicious activity on social networks. “The applicability of Benford’s Law to social media is a new tool for analyzing user behavior, understanding when and why natural deviations may occur, and ultimately detecting when abnormal forces are at work,” concludes Golbeck.

Ref: arxiv.org/abs/1504.04387 : Benford’s Law Applies to Online Social Networks