Astrophysicists Prove That Cities On Earth Grow in the Same Way As Galaxies in Space
Urban sociologists have long known that a set of remarkable laws govern the large-scale interaction between individuals such as the probability that one person will befriend another and the size of the cities they live in.
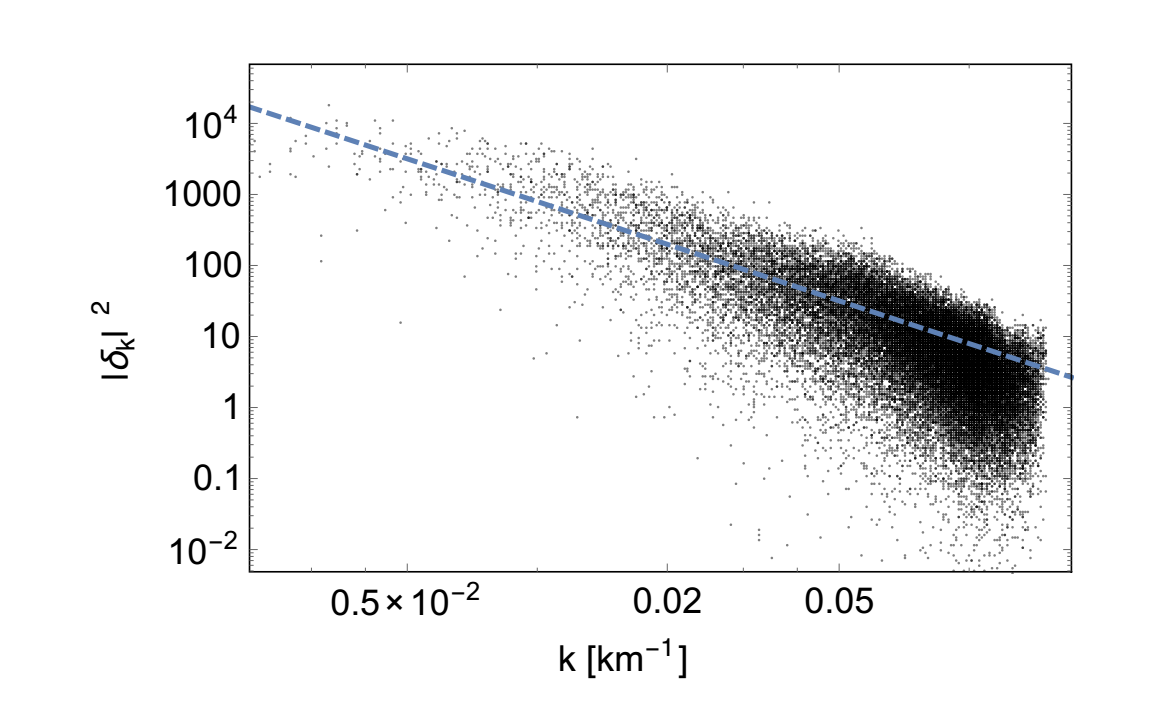
The latter is an example of the Zipf’s law. If cities are listed according to size, then the rank of a city is inversely proportional to the number of people who live in it. For example, if the biggest city in the US has a population of 8 million people, the second-biggest city will have a population of 8 million divided by 2, the third biggest will have a population of 8 million divided by 3 and so on.
This simple relationship is known as a scaling law and turns out to fit the observed distribution of city sizes extremely well.
Another interesting example is the probability that one person will be friends with another. This turns out to be inversely proportional to the number of people who live closer to the first person than the second.
What’s curious about these laws is that although they are widely accepted, nobody knows why they are true. There is no deeper theoretical model from which these laws emerge. Instead, they come simply from the measured properties of cities and friendships.
Today, all that changes thanks to the work of Henry Lin and Abraham Loeb at the Harvard-Smithsonian Centre for Astrophysics in Cambridge. These guys have discovered a single unifying principle that explains the origin of these laws.
And here’s the thing: their approach is mathematically equivalent to the way that cosmologists describe the growth of galaxies in space. In other words, cities form out of variations in population density in exactly the same way that galaxies formed from variations in matter density in the early universe.
These guys begin by creating a mathematical model of the way human population density varies across a flat Euclidean plane. (They say they can ignore the effects of the Earth’s curvature in their model because any variations in population density will be small compared to the radius of the Earth.)
That is exactly how cosmologists think about the way galaxies evolved. They first consider the matter density of the early universe. Next, they look at the mathematical structure of any variations in this density. And finally they use this mathematics to examine how this density can change over time as more matter is added or taken away from specific regions.
Because of the many decades of work on cosmology, these mathematical tools are already well understood and easily applied to the similar problem of the population density on Earth. All that is needed is some data to calibrate the mathematical model.
For example, the time it takes for any perturbations in the population density to smooth themselves out is of the order of five years. That’s the timescale over which about 35 percent of people in the US change residences.
Having created a model of the way that population density varies, Lin and Loeb test the model against publicly available data. “The results are in good agreement with the theoretical prediction across a broad range of spatial scales, from a few km to ∼ 10^3 km,” they say.
They go on to calculate the number of cities above a certain population threshold and show using the model that this quantity has a logarithmic slope equal to -1. “This statement is equivalent to Zipf’s law: the rank of a city is inversely proportional to its size,” point out Lin and Loeb.
They also calculate the average number of friends a person might have within a given region. And once again their model comes up with the inverse-rank friendship law that urban sociologists are already familiar with.
Interestingly, they say their model leads to the same laws for a wide range of initial conditions. That’s important because the models do not require any fine-tuning to match the observed data, a problem that cosmologists are frustratingly well versed in.
The work of Lin and Loeb is not just a mathematical curiosity. It has important implications for other factors that are related to population density, such as the spread of disease. Indeed, they say their model points to a new way of determining how disease spreads based on a parameter they call the bias factor, which ought to be observable in historical data on epidemics.
“Just as the development of models for non-linear structure formation in the universe led to a wealth of theoretical and observational work in cosmology, future work here could include the calculation of new observables such as the bias factor for the spread of epidemics,” they conclude.
That’s a fascinating piece of science that leads to a unified theory of urban evolution for the first time.
Ref: http://arxiv.org/abs/1501.00738 : A Unifying Theory for Scaling Laws of Human Populations
Keep Reading
Most Popular
Large language models can do jaw-dropping things. But nobody knows exactly why.
And that's a problem. Figuring it out is one of the biggest scientific puzzles of our time and a crucial step towards controlling more powerful future models.
How scientists traced a mysterious covid case back to six toilets
When wastewater surveillance turns into a hunt for a single infected individual, the ethics get tricky.
The problem with plug-in hybrids? Their drivers.
Plug-in hybrids are often sold as a transition to EVs, but new data from Europe shows we’re still underestimating the emissions they produce.
Google DeepMind’s new generative model makes Super Mario–like games from scratch
Genie learns how to control games by watching hours and hours of video. It could help train next-gen robots too.
Stay connected
Get the latest updates from
MIT Technology Review
Discover special offers, top stories, upcoming events, and more.