Benford’s Law And The Art of Succeeding in Multiple Choice Tests
Back in the 1930s, the American physicist Frank Benford discovered that the first digit in certain lists of numbers was much more likely to be a 1 than a 9. He tested this idea on a variety of datasets such as the surface area of rivers, a list of physical constants and even the street addresses of the first 342 entries in American Men of Science.
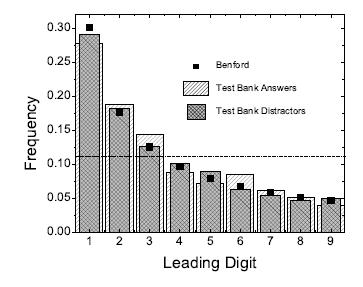
In each case, he found the same pattern. That the number 1 is the first digit 30 per cent of the time, the number 2 is the first digit 18 per cent of the time, the number 3 is first 13 per cent of the time and so on until the number 9 which is first only 5 per cent of the time.
He went on to propose Benford’s Law: that the distribution of first numbers in many, but not all, datasets follows the same logarithmic pattern. It turns out that this property is true of many dataset involving physical quantities but is not true of randomly generated numbers in which the distribution of first digits is uniform.
Now, 60 years later, Benford’s law is famous. It’s best known application is in uncovering fraud. That’s possible because the distribution of first digits in a company’s accounts turns out to follow Benford’s law. So any deviation from this is good evidence that somebody has been cooking the books. And this has led to the downfall of various fraudsters.
But that raises an interesting question: where else might Benford’s law be put to good use?
Today, Aaron Slepkov at Trent University in Peterborough, Canada, and a couple of pals put forward a suggestion. They point out that the answers to multiple choice examination papers in physics must follow Benford’s law. But if the incorrect answers are chosen at random, they will not follow Benford’s law.
So can an enterprising student with an understanding if Benford’s law, but little understanding of physics, gain an advantage?
To find out, Slepkov and co simulated such a multiple choice exam involving 5000 mock questions. For the correct answers, they used a dataset of numbers taken from the answers to real physics questions. But they took the incorrect answers from a dataset of random numbers in which the first digits are uniformly distributed (i.e. the first digit is equally likely to be any of the digits from 1 to 9).
The best strategy in such a multiple choice test is to choose the answer with the lowest first digit. And when two or more answers have the same lowest digit, then pick.
And that’s what Slepkov and co did in taking the tests. The results are conclusive. In a multiple choice test involving 3 possible answers, this strategy produced a score of 51 per cent. That’s a clear pass even though the answers were chosen without any knowledge of the physics being tested.
In a sense, that’s not really surprising. Benfords’ law implies that chances of the first digit being a 1, 2 or 3 are greater than 50 per cent and this produces a clear bias for somebody in the know.
But does this strategy work for real exams? Slepkov and co tested it on a dataset of well-known physics multiple choice exams and their results throw up a surprise.
The strategy suggested by Benford’s law gives no advantage whatsoever. They found that it was impossible to pass a physics exam in this way.
How come? Slepkov and co took a closer look at the correct answers and the dummy answers as well in these papers and found something surprising. While the real answers follow Benford’s law, the incorrect answers do as well. So there’s no difference in the distribution of first digits that an enterprising student can exploit.
Exactly why the incorrect answers follow Benford’s law isn’t clear. They’re obviously not random numbers so how can they been chosen? Slepkov and co discuss a number of possibilities, perhaps the most obvious being that they are answers to other questions and so are themselves physical quantities. But there are other possibilities too.
That will be a disappointment to the legions of physics students reading this who were hoping to get by with little or no knowledge of their subject.
For these students, Slepkov and co offer a sliver of hope. They point out that the chances of a correct answer to a physics question starting with the digits 1, 2 or 3 is over 50 per cent. But equally, the chances of the answer starting with a 7, 8 or 9 is only 15 per cent.
So they conclude with this:
“One trifling piece of advice we can give to the test-wise student is as follows: At the end of a long constructed-response examination, if you have little time to double-check the answers to all of the questions, spend time on those questions that yielded final answers that have the largest leading digits; questions are expected to have answers with leading digits 7, 8, or 9 only 15% of the time.”
Good luck!
Ref: arxiv.org/abs/1311.4787v1 : Benford’s Law: Textbook Exercises and Multiple-choice Testbanks
Keep Reading
Most Popular
Large language models can do jaw-dropping things. But nobody knows exactly why.
And that's a problem. Figuring it out is one of the biggest scientific puzzles of our time and a crucial step towards controlling more powerful future models.
The problem with plug-in hybrids? Their drivers.
Plug-in hybrids are often sold as a transition to EVs, but new data from Europe shows we’re still underestimating the emissions they produce.
How scientists traced a mysterious covid case back to six toilets
When wastewater surveillance turns into a hunt for a single infected individual, the ethics get tricky.
Google DeepMind’s new generative model makes Super Mario–like games from scratch
Genie learns how to control games by watching hours and hours of video. It could help train next-gen robots too.
Stay connected
Get the latest updates from
MIT Technology Review
Discover special offers, top stories, upcoming events, and more.