One of the increasingly famous paradoxes in science is named after the German mathematician Dietrich Braess who noted that adding extra roads to a network can lead to greater congestion. Similarly, removing roads can improve travel times.

Traffic planners have recorded many examples of Braess’ paradox in cities such as Seoul, Stuttgart, New York and London. And in recent years, physicists have begun to study how it might be applied in other areas too, such as power transmission, sporting performance where the removal of one player can sometimes improve a team’s performance and materials science where the network of forces within a material  can be modified in counterintuitive ways, to make it expand under compression, for example.

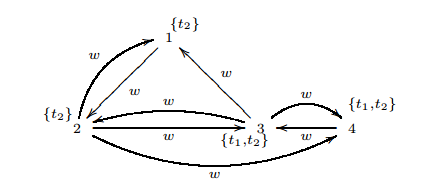
Today,  Krzysztof Apt at the University of Amsterdam in The Netherlands and a couple of pals reveal an entirely new version of this paradox that occurs in social networks in which people choose products based on the decisions made by their friends. 

They show mathematically that adding extra products can reduce the outcome for everyone and that reducing product choice can lead to better outcomes for all. That’s a formal equivalent to Braess’ paradox for consumers.

Although that seems counterintuitive, it’s not so hard to imagine. Many people will have had the experience of choosing a computer, for example, where there is so much choice that it is impractical to research and assess all the available options. This reduces the chances of  making the optimal choice and everyone is worse off.

Similarly everybody ends up better off in this example when the number of choices is reduced. 

What Apt and co have done is analysed this in a formal mathematical setting–indeed in this mathematical world, a number of other paradoxes emerge as well. 

That’s interesting because it could have an important effect on market dynamics. Traffic planners already use this kind of network approach to work out how to improve the traffic flow through cities by either opening or closing roads.

So it’s not hard to imagine a mathematical model that tells product designers when to launch and remove products form the market in a way that improves the outcome for everybody.  

Ref: arxiv.org/abs/1301.7592 :Paradoxes in Social Networks with Multiple Products