Quantum Entanglement Can be a Measure of Free Will
The nature of quantum mechanics has forced researchers to reconsider their own role in the process of science. Gone is the Victorian idea that measurement is objective and absolute. Today, we know that in the quantum world, it is impossible to separate the measured from the measurer. But exactly what role measurement plays in the universe, we have yet to fathom.
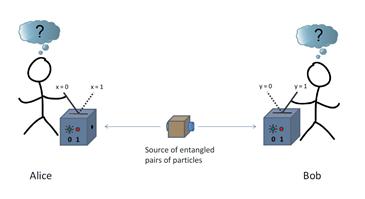
One intriguing idea is that certain kinds of experiments can tease apart the nature of measurement. And one particularly important class of experiment involves quantum entanglement, the hugely puzzling phenomenon in which widely separated objects share the same existence (or in scientific terms, are described by the same wave function).
Imagine two particles that are entangled in this way. Before any measurement takes place, these particles are in a superposition of states. Then a measurement on one immediately influences the other, somehow determining the outcome of a measurement on it.
Many experiments have shown that this “influence” happens as close to instantaneously as it is possible to measure and certainly cannot be mediated by any lightspeed signal. The same experiments also rule out any hidden correlation between the particles in which the outcome of any measurement is agreed upon in advance. Imagine, for example, some unseen hand that forces experimenters to unknowingly carry out measurements that always make it look as if this spooky action at a distance was taking place.
Today, Jonathan Barrett from the University of Bristol and Nicolas Gisin from the University of Geneva provide us with an interesting new take on this problem. They assume that entanglement does occur as quantum mechanics proscribes and then ask how much free will an experimenter must have to rule out the possibility of hidden interference.
The answer is curious. Barret and Gisin prove that if there is any information shared by the experimenters and the particles they are to measure, then entanglement can be explained by some kind of hidden process that is deterministic.
In practical terms, this means that there can be no shared information between the random number generators that determine the parameters of the experiments to be made, and the particles to be measured.
But the same also holds true for the experimenters themselves. It means there can be no information shared between them and the particles to be measured either. In other words, they must have completely free will.
In fact, if an experimenter lacks even a single bit of free will then quantum mechanics can be explained in terms of hidden variables. Conversely, if we accept the veracity of quantum mechanics, then we are able to place a bound on the nature of free will.
That’s an interesting way of stating the problem of entanglement and suggests a number of promising, related conundrums: what of systems that are partially entangled and others in which more than two particle become entangled.
Free will never looked so fascinating.
Ref: arxiv.org/abs/1008.3612: How Much Free Will Is Needed To Demonstrate Nonlocality?
Keep Reading
Most Popular
Large language models can do jaw-dropping things. But nobody knows exactly why.
And that's a problem. Figuring it out is one of the biggest scientific puzzles of our time and a crucial step towards controlling more powerful future models.
How scientists traced a mysterious covid case back to six toilets
When wastewater surveillance turns into a hunt for a single infected individual, the ethics get tricky.
The problem with plug-in hybrids? Their drivers.
Plug-in hybrids are often sold as a transition to EVs, but new data from Europe shows we’re still underestimating the emissions they produce.
Google DeepMind’s new generative model makes Super Mario–like games from scratch
Genie learns how to control games by watching hours and hours of video. It could help train next-gen robots too.
Stay connected
Get the latest updates from
MIT Technology Review
Discover special offers, top stories, upcoming events, and more.