Theoretical Breakthrough for Quantum Cryptography
The world of cryptography is currently undergoing a quantum revolution. The weird laws of quantum mechanics allow cryptographers to create codes that guarantee perfect secrecy. Until recently, the best cryptographers could aim for was just pretty good secrecy with codes that were always compromised in some way or another. Quantum cryptography, on the other hand, is perfect: theoretically and practically secure.
A few companies have even sprung up to sell the gear that can send perfectly secure messages, mainly to banks and governments (although the gear itself creates some loopholes that eavesdroppers can attack).
But it’s still early days for this technology and naturally it suffers from several drawbacks. For example, one well known limitation is that quantum cryptography can only be used over point-to-point connections and not through networks where data has to be routed. That’s because the routing process destroys the quantum properties of the photons used to secure messages.
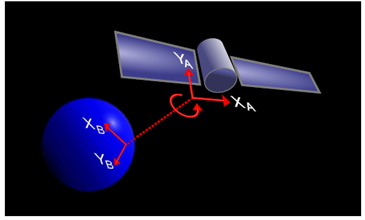
A lesser known limitation is that the sender and receiver of quantum encrypted messages–the famous Alice and Bob–must be perfectly aligned so that they can carry out well-defined polarisation measurements on the photons as they arrive. Physicists say that Alice and Bob must share the same reference frame.
That’s not so hard to do when Alice and Bob are both based in labs on the ground. But it’s much harder when one or the other is moving, in a satellite, for example, which would be both spinning and orbiting the Earth.
Today, Anthony Laing from the University of Bristol and a few pals show how to get round this. The trick is to use entangled triplets of photons, so-called qutrits, rather than entangled pairs.
This solves the problem by embedding it in an extra abstract dimension, which is independent of space. So as long as both Alice and Bob know the way in which all these abstract dimensions are related, the third provides a reference against which measurements of the other two can be made.
That allows Alice and Bob to make any measurements they need without having to agree ahead of time on a frame of reference. There is one proviso: Alice and Bob cannot move too quickly during the measurements since this changes their relative orientation and a new qutrit will be needed to establish a reference.
That’ll be useful for quantum encryption over satellite links, the kind of thing that government agencies and the military might want to do. But there’s another, more valuable application.
If quantum encryption is ever to be widely used, it’ll need to work between one microchip and another without the need to share a frame of reference in advance. That’s always been a problem because the chips inside computers are constantly on the move (relative the the wavelength of light) and because photon polarisations drift as they move through optical fibres, introducing another source of error.
That’s why quantum cryptography that is reference frame independent is an enabling technology and so potentially hugely valuable. It means that Laing and co may have made one of the key breakthroughs that will bring quantum cryptography to the masses.
Ref: arxiv.org/abs/1003.1050: Reference Frame Independent Quantum Key Distribution
Update: Anthony Laing writes:
I have a few clarifications which may be useful for your readers…
- The protocol is always bipartite - so two people, two particles,
one particle each.
- The protocol works best for particle dimensions of prime or power-
prime, including the 2 dimensional qubit, so an entangled pair of
qubits is the most simple case that works.
- The protocol works because security is guaranteed with a purity
measure on the joint ‘entangled’ space of Alice and Bob and this
purity would not be reduced too much in a reference frame that varies
slowly on the timescale of rate-of-pair-creation and measurement.
Keep Reading
Most Popular
Large language models can do jaw-dropping things. But nobody knows exactly why.
And that's a problem. Figuring it out is one of the biggest scientific puzzles of our time and a crucial step towards controlling more powerful future models.
The problem with plug-in hybrids? Their drivers.
Plug-in hybrids are often sold as a transition to EVs, but new data from Europe shows we’re still underestimating the emissions they produce.
Google DeepMind’s new generative model makes Super Mario–like games from scratch
Genie learns how to control games by watching hours and hours of video. It could help train next-gen robots too.
How scientists traced a mysterious covid case back to six toilets
When wastewater surveillance turns into a hunt for a single infected individual, the ethics get tricky.
Stay connected
Get the latest updates from
MIT Technology Review
Discover special offers, top stories, upcoming events, and more.