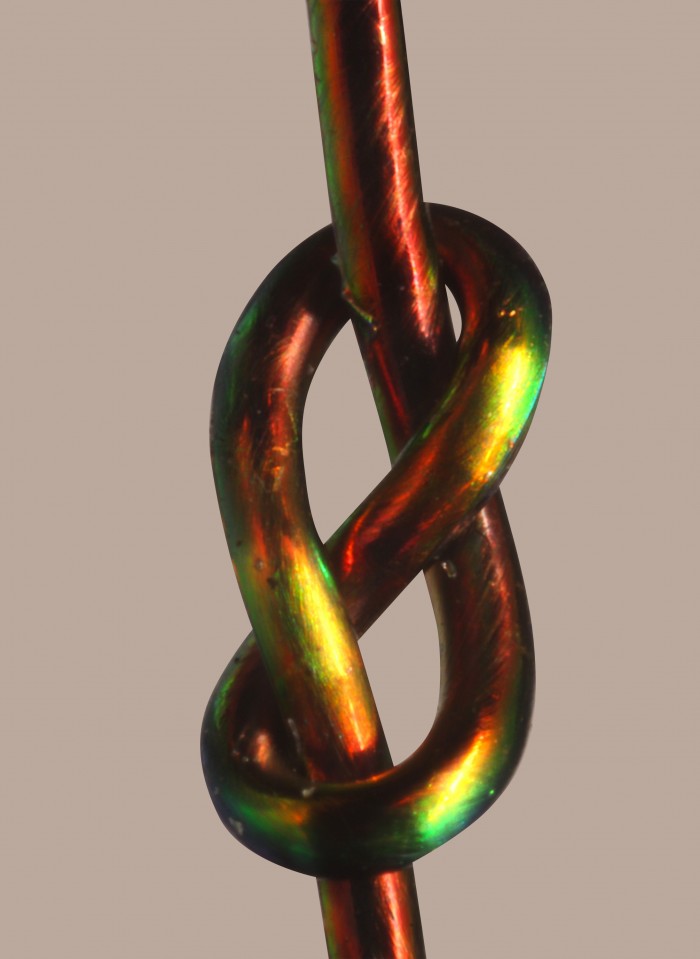
Any seasoned sailor knows that one type of knot will secure a sheet to a headsail, while another is better for hitching a boat to a piling. But what exactly makes one knot more stable than another was not well understood—until associate professor of mathematics Jörn Dunkel created a mathematical model to study them.

Dunkel teamed up with Mathias Kolle, an associate professor of mechanical engineering, whose group had engineered stretchable fibers that change color in response to strain or pressure. His team used Kolle’s fibers to tie a variety of knots, including trefoils and figure-eights, photographing each fiber and noting where and when it changed color, along with the forces applied as it was pulled tight.

Using this data, they calibrated a model simulating the distribution of stress in knots. Then they simulated more complicated knots and drew up simple diagrams to represent them.

In comparing diagrams for the common granny, reef, thief, and grief knots, along with more complicated ones such as the carrick, zeppelin, and Alpine butterfly, the researchers identified some general rules. Basically, a knot is stronger if it has more strand crossings, as well as more “twist fluctuations”—changes in the direction each segment of a strand rotates as a knot is tightened. These changes create friction that promotes stability.

They also found that a knot can be made stronger if it has more “circulations”—regions where two parallel strands loop against each other in opposite directions.

“If you take a family of similar knots from which empirical knowledge singles one out as ‘the best,’ now we can say why it might deserve this distinction,” says Kolle. “We can play knots against each other for uses in suturing, sailing, climbing, and construction.”