Warning: This Algorithm Will Self-Destruct After It’s Used
Imagine two millionaires—Alice and Bob—who want to decide who is the richer but without revealing their wealth. How do they go about solving their conundrum? This is Yao’s Millionaire Problem, devised by the computer scientist Andrew Yao in 1982.
One potential solution is a one-time computer program. This program allows Alice and Bob to enter their data privately, performs the calculation once, gives the answer and then destroys itself. This ensures that nobody can access the original data or the way it was processed. And it gives Alice and Bob their answer without compromising their financial details.
Computer security experts say that one-time programs are a hugely important tool in cybersecurity. Or they would be, if anybody could build them.
It turns out that it is impossible to build an ideal one-time program that runs once and then destroys itself. A classical computer of this kind would have to be physically destroyed to ensure it cannot be used again, and there is no known way of guaranteeing this.
A quantum computer might seem to offer more potential, since quantum information is easily destroyed and impossible to copy. But it turns out that a quantum computer cannot give a deterministic answer to a one-off calculation.
So the dream of a one-time program that destroys itself after a single calculation seems doomed.
Enter Marie-Christine Roehsner at the University of Vienna and Joshua Kettlewell at the National University of Singapore and a few pals. Today, they say they’ve found a way to build a one-time program and have built and demonstrate a proof-of-principle device for the first time.
The new method relies on a different way of thinking about one-time programs performed by quantum computers. Until now, security experts have always expected a definitive solution: Bob’s worth is either more or less than Alice’s.
But quantum mechanics is an inherently probabilistic process, and that means it can only give the correct answer within certain limits of probability, say 75 percent of the time. As long as Alice and Bob are willing to accept the possibility of an error in the calculation, then it is possible to guarantee that their information will remain secure, that the program runs once only and then destroys itself.
“We relax the definition of one-time programs to allow some probability of error in the output and show that quantum mechanics offers security advantages over purely classical resources,” say the researchers.
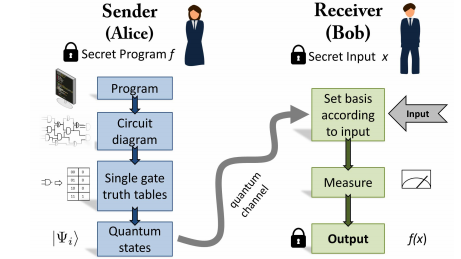
The approach is straightforward. Alice secretly encodes her wealth in the states of a set of qubits stored in a quantum computer. This computer is programmed to compare this number with one entered by Bob and to tell him whether his wealth is greater or less than Alice’s.
This quantum processing is itself an irreversible process, and this prevents Bob from entering other numbers to determine Alice’s wealth.
But the hardware is fixed and a potential weakness of this approach is that Bob can reverse-engineer the program by working out how the logic gates are wired.
Roehsner and co have a trick to prevent this, though. Although they can’t hide the physical wiring, they can hide the truth tables that govern the behavior of each logic gate. “This is because our approach is to encode the truth table for individual gates as a one-time program in its own right,” they say.
This allows Alice’s information to be encoded in the precise choice of logic gates and not on the connections between them. In this way it remains hidden from Bob.
Roehsner and co have tested this idea in a proof-of-principle experiment. This encodes information in the polarization of photons and processes it using various kinds of optical logic gates. The average probability of success for each of the gates is 75 percent, which the team says is in good agreement with the expected value.
The team then used this set up to solve Yao’s Millionaire problem for numbers consisting of four bits that differ by a single bit. The program works by comparing each bit to decide which is larger.
The results make for interesting reading. The team says the probability of success increases with the number of bits used for error correction, but this also reduces the security of the system. So there is a clear trade-off between accuracy and security. Nevertheless, the team says the security is better than can be achieved with classical computing alone.
“Our results demonstrate that quantum physics allows for better security trade-offs for certain secure computing tasks than are possible in the classical world, even when perfect security cannot be achieved,” they say.
What’s more, the method is workable with current technology, and relatively modest advances should increase security further.
That’s interesting work that shows the potential of quantum technologies to dramatically increase security using technology that is available today. “We believe the presented work strongly hints at a rich area of quantum protocols to enhance the security of classical computation, even before large-scale quantum computers can be realized,” say Roehsner and co.
It’ll be interesting to see how the work is received.
Ref: arxiv.org/abs/1709.09724: Quantum Advantage for Probabilistic One-Time Programs
Keep Reading
Most Popular
Large language models can do jaw-dropping things. But nobody knows exactly why.
And that's a problem. Figuring it out is one of the biggest scientific puzzles of our time and a crucial step towards controlling more powerful future models.
How scientists traced a mysterious covid case back to six toilets
When wastewater surveillance turns into a hunt for a single infected individual, the ethics get tricky.
The problem with plug-in hybrids? Their drivers.
Plug-in hybrids are often sold as a transition to EVs, but new data from Europe shows we’re still underestimating the emissions they produce.
Google DeepMind’s new generative model makes Super Mario–like games from scratch
Genie learns how to control games by watching hours and hours of video. It could help train next-gen robots too.
Stay connected
Get the latest updates from
MIT Technology Review
Discover special offers, top stories, upcoming events, and more.