First Experimental Demonstration of a Quantum Enigma Machine
One of the great unsung heroes of 20th century science was a mathematician and engineer at the famous Bell Laboratories in New Jersey called Claude Shannon. During the 1940s, ‘50s and ‘60s, Shannon laid the mathematical foundations for modern communications and computing while building some of the first intelligent machines.
Along the way, he also made a major contribution to the theory of cryptography with a paper entitled Communication Theory of Secrecy Systems, published in 1949. In it, he proved it possible to send a perfectly secure message provided that the encryption key is entirely random and used only once.
Shannon’s work is the mathematical proof that the one-time pad is a truly unbreakable form of encryption. A critical condition is that the encryption key must be at least as long as the message itself.
Shannon’s work assumes that the message is sent using conventional forms of transmission. But in the last 10 years, quantum physicists have shown that it is possible to do better if the message is encrypted using quantum rules. In particular, they have shown that in the quantum world, a secure message can be sent with a key that is significantly shorter than the message itself. At least in theory.
Researchers have christened this device a “quantum enigma machine,” after the Nazi encryption device that codebreakers led by Alan Turing cracked during the Second World War. But the device has been entirely theoretical.
Until now. Today, Daniel Lum at the University of Rochester in New York State and a few pals unveil an actual working quantum enigma machine for the first time. Their proof-of-principle device is capable of sending perfectly secure messages using a key that is shorter than the message itself.
A one-time pad works by adding a random number to each digit in a message. That makes the message indistinguishable from a randomness. It can only be read by subtracting the same random numbers to produce the original message.
The secrecy depends on the transmitter and receiver being the only people with the list of random numbers. And of course this list must be longer than the message itself.
The quantum version of this process works by encoding information in a quantum object such as a photon and then altering the state of the photon with a random operation. The information can only be retrieved by reversing the random operation. So as long as only the transmitter and receiver know the sequence of random operations—the quantum key—and that this key is used only once, the message is perfectly secure.
However, quantum theorists have shown that the quantum key can be exponentially shorter than the message itself.
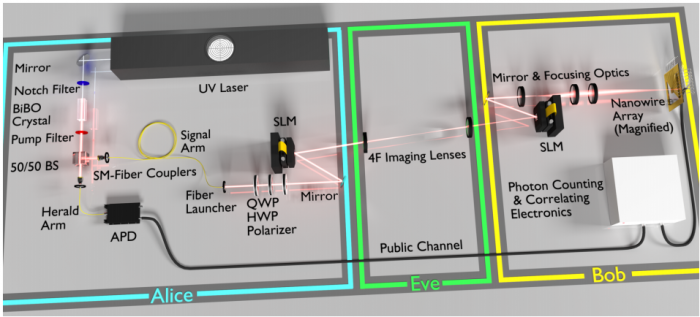
Now Lum and co have built a transmitter and receiver that exploits this mechanism. Their device consists of a photon gun that fires single photons through a kind of mask called a spatial light modulator which superimposes information onto the photon’s wavefront. If this modulator consists of an 8 x 8 array, it can encode 64 bits of information. At the same time, the spatial light modulator adds a random signal to the information it transmits.
The important point is that all the information encoded on the photon is randomized by a random signal. So the sequence of random signals used for encryption can be significantly shorter than the message itself.
That allows an important twist. Because the message is shorter than the key, it is also possible to send a new key for encoding the next message. In this way, the message and the new key are sent at the same time and both are kept entirely secret.
The receiver detects each photon using a light sensitive array that can pick out the pattern superimposed on the photon. It then subtracts the random signal leaving the original message.
Lum and co have done exactly this. “We demonstrated the phenomenon with a proof-of-principle experiment to lock 6 bits per photon while using less than 6 bits per photon of secret key,” says the team. In other words, these guys have built the first proof-of-principle quantum enigma machine.
That’s an interesting result that has immediate application. Physicists already use quantum mechanics to send perfectly secure messages using a technique called quantum key distribution. The techniques for doing this are becoming increasingly advanced. Indeed, there are already commercial versions of this kind quantum encryption on the market.
Lum and co say that the technology and techniques developed for quantum key distribution can be immediately applied to building quantum enigma machines. So there’s no reason why the technique cannot be commercialized in the near future. Shannon would surely be impressed.
Ref: arxiv.org/abs/1605.06556: A Quantum Enigma Machine: Experimentally Demonstrating Quantum Data Locking
Deep Dive
Computing
How ASML took over the chipmaking chessboard
MIT Technology Review sat down with outgoing CTO Martin van den Brink to talk about the company’s rise to dominance and the life and death of Moore’s Law.
How Wi-Fi sensing became usable tech
After a decade of obscurity, the technology is being used to track people’s movements.
Why it’s so hard for China’s chip industry to become self-sufficient
Chip companies from the US and China are developing new materials to reduce reliance on a Japanese monopoly. It won’t be easy.
Stay connected
Get the latest updates from
MIT Technology Review
Discover special offers, top stories, upcoming events, and more.