Machine-Learning Algorithm Calculates Fair Distance for a Race Between Usain Bolt and Long-Distance Runner Mo Farah
It’s obviously unfair to compare the performance of sprinters and long-distance runners. These endeavors place entirely different demands on the body, which is why good sprinters are entirely unsuited to the demands of marathon running and distance runners perform poorly in sprints.
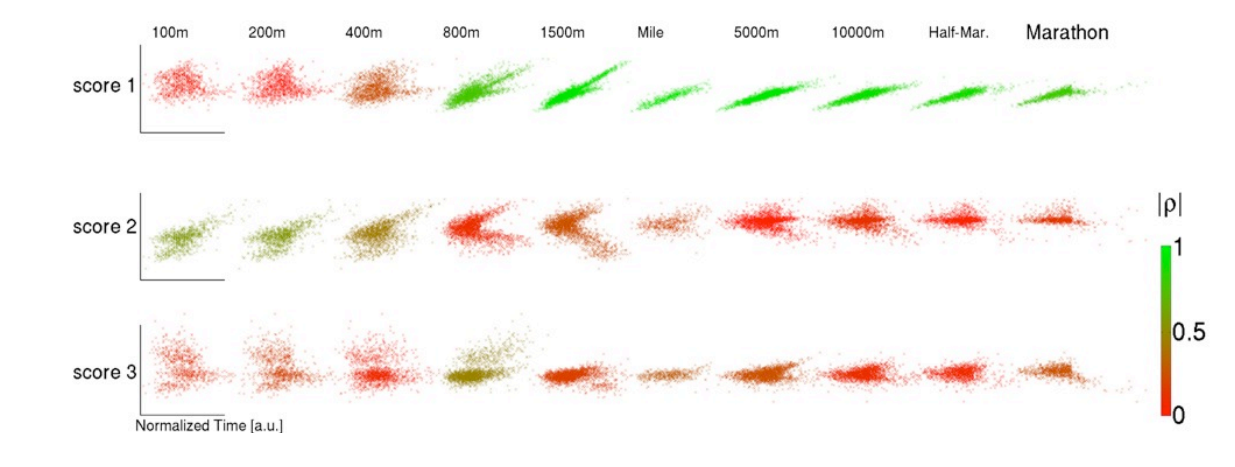
But where does the crossover point lie? What distance would represent a fair race between the two extremes—for example, between 100-meter world record holder Usain Bolt and Olympic 10,000-meter gold medalist Mo Farah?
Today, we get an answer thanks to the work of Duncan Blythe at Humboldt University of Berlin and Franz Király at University College London. These guys have developed a new model that accounts for the different kinds of athletic performance required for short, middle, and long-distance running.
The model even predicts an athlete’s performance at one distance given his or her performance at others. Which is how they’ve come up with the perfect distance at which Bolt and Farah could race fairly.
Sport scientists have long known that the world records for running various distances follow a power law. When Usain Bolt set the record for the 100 meters in August 2009, he ran at an average speed of just over 10 meters per second. The world-record speed for the mile is just over seven meters per second. And in 2014, the Kenyan runner Dennis Kimetto set the world record for the marathon by running at a speed of just under six meters per second over 42 kilometers.
In other words, a small increase in average speed dramatically reduces the distance at which a world record is possible. But the link between speed and distance is actually more complex than this.
When researchers plot world-record speeds against distance, it produces a power-law curve with a curious kink in its shape. It’s almost as if one power law governs running speeds over distances shorter than a mile while another governs running speeds at longer distances.
The conventional explanation for this is that sprinters burn energy anaerobically while long-distance runners burn it aerobically. The kink occurs at the crossover in an athlete’s energy expenditure.
The problem with this model is that it has limited predictive power. Given a sprinter’s performance at short and middle distances, the model has nothing to say about how good he or she will be at long-distance running. It is similarly silent about a marathon runner’s sprinting ability.
This is where Blythe and Király’s work comes in. These guys started with a huge database of athletic performance since 1954 in Britain. They take the times and distances of almost 1.5 million individual performances by both genders ranging from the amateur to the elite, both young and old. These records apply to 10 different distances: 100 meters, 200 meters, 400 meters, 800 meters, 1,500 meters, the mile, 5 kilometers, 10 kilometers, the half-marathon (21 kilometers), and the full marathon of 42 kilometers.
Then they used a machine-learning algorithm to find an equation that best fits the data in a way that predicts an individual’s performance at one distance, given his or her performance at other distances. This equation also has to produce the famous “broken” power law that describes the distribution of world-record performances.
It’s not hard to find equations that describe almost any distribution. All that is needed is as many additional parameters as necessary to tweak the curve in the right way. And sure enough, the machine found such an equation.
But the surprise is that this equation uses only three parameters to describe the performance of every individual in the database.
The first parameter in this model is an ordinary power law, which describes an individual’s overall performance. This is something of a surprise given the distribution of world records. However, the other two components modify this power law in a way that reproduces the broken power law.
The second parameter describes whether an athlete has greater endurance or greater speed. And the third parameter describes whether an athlete is better at middle distances rather than short or long distances.
Together, these three parameters completely describe an athlete’s individual performance over all distances, leading to an entirely new model of athletic capability. “Our analysis provides strong evidence that the three-number summary captures physiological and/or social/behavioural characteristics of the athletes, e.g., training state, specialization, and which distance an athlete chooses to attempt,” say Blythe and Király.
Having discovered and tested this model, Blythe and Király use it to gain insight for the first time into a number of important questions for athletes. For example, one question that marathon runners have long pondered is whether it is better to develop a higher maximum speed or to build endurance.
Blythe and Király say their model gives a clear answer: “There is only one way to be a fast marathoner, i.e., possessing a high level of endurance—as opposed to being able to coast relative to a high maximum speed,” they say.
The model also suggests that a runner who is not world-class over 10 kilometers is unlikely to be world-class over the marathon distance of 42 kilometers.
The researchers are even able to make predictions about individual athletes. One of these is Kenenisa Bekele, an Ethiopian long-distance runner who holds the world records at both 5,000 meters and 10,000 meters. Blythe and Király say their model predicts that Bekele should be able to run a marathon in 2:00:36, almost three minutes faster than the current world record.
And what of the original question about a fair distance for a race between long-distance runners and sprinters? Blythe and Király have an answer here too. “We predict that a fair race between Mo Farah and Usain Bolt is over 492m,” they say.
Now that’s a race worth waiting for.
Ref: arxiv.org/abs/1505.01147 : Prediction and Quantification of Individual Athletic Performance
Keep Reading
Most Popular
Large language models can do jaw-dropping things. But nobody knows exactly why.
And that's a problem. Figuring it out is one of the biggest scientific puzzles of our time and a crucial step towards controlling more powerful future models.
The problem with plug-in hybrids? Their drivers.
Plug-in hybrids are often sold as a transition to EVs, but new data from Europe shows we’re still underestimating the emissions they produce.
Google DeepMind’s new generative model makes Super Mario–like games from scratch
Genie learns how to control games by watching hours and hours of video. It could help train next-gen robots too.
How scientists traced a mysterious covid case back to six toilets
When wastewater surveillance turns into a hunt for a single infected individual, the ethics get tricky.
Stay connected
Get the latest updates from
MIT Technology Review
Discover special offers, top stories, upcoming events, and more.