Cosmic Rays, Neutrons And The Mutation Rate In Evolution

When cosmic rays hit the upper atmosphere, they send high-energy particles, such as neutrons, showering down towards the surface. So an interesting question is how these neutrons influence things on the ground.

Researchers have long known that high-energy neutrons can smash into atomic nuclei causing all kinds of damage to the structure of materials. This is one cause of errors in computer memories.

Indeed, back in 2004, a group of researchers from IBM measured the flux of neutrons from cosmic ray collisions and used their results to predict the error rate in computer memories another electronic logic devices. Their predictions closely matched the observed rate of error, suggesting that neutrons are indeed an important source of problems in computing.

That finding has captured the imagination of Augusto González at the Institute of Cybernetics, Mathematics and Physics in Havana, Cuba. If background neutron radiation can cause errors in computer circuitry, then it ought to have a similarly destructive effect on another much more common information processing system–life.

Evolutionary biologists have long known that spontaneous mutations occur at a rate that has a crucial influence on the nature of evolution. But exactly what causes spontaneous mutation has never been properly understood.

Now González says that same approach that the IBM researchers used to predict errors in computer memory also explains the rate of spontaneous mutations in living things.

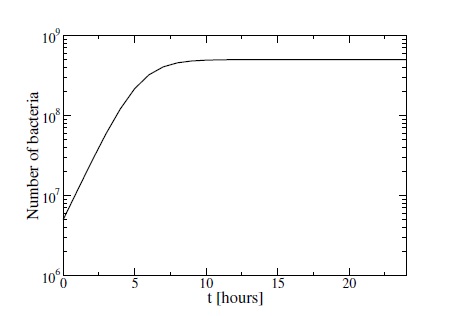
González bases his work on a fascinating experiment carried out by Richard Lenski and his team at Michigan State University that has been ongoing since 1988. These guys have been growing the bacteria, E. coli, since then and monitoring the mutations that occur between generations.

Every day, a small amount of bacteria is taken from one culture and allowed to grow in a new dish of glucose over the course of the following day. The bacteria reproduce until the glucose runs out, usually within eight hours or so. A small amount of bacteria is taken from this dish and allowed to grow in a new one and so on.

Since 1988, the team has observed how the bacteria have evolved over 60,000 generations. And they’ve discovered that the number of point mutations in the bacteria after 20,000 generations is about 300 million. That’s a rate of about 1 per second.

The question that González addresses is whether this mutation rate can be explained by the background neutron radiation. He does this by creating a mathematical model of the environment in which bacteria grow, which is essentially water.

He calculates that high-energy neutron would enter the water on a bacterial sample about once every 125 seconds. This high-energy neutron would then transfer its energy to water molecules creating a relatively short track of ions. He says that a single neutron would generate some 300 ions over a track length of about 100 nanometers and about 30 ions at a distance of 0.1 mm

“The bacteria touched by this ion shower could be destroyed or experience a permanent damage, especially in their DNA, which can be later inherited by the descendants,” he says.

The question then is how often this happens. And he calculates that this rate is consistent with the frequency of deleterious mutations measured in Lenski’s experiments. “In this way, we are indicating the probable origin of a class of “spontaneous” mutations,” he says.

Of course, González is pointing out a correlation between background neutron radiation and the observed rate of deleterious mutations in E. coli. That’s only part of what is required for scientific confirmation.

What’s needed next is some good old-fashioned experimental work that confirms the correlation. And González explains how this can be done in an experiment that is simple, at least in principle. Simply repeat Lenski’s long-term evolution experiments but with two populations of bacteria, one of which is shielded from background neutron radiation. “The shielded cultures should exhibit much lower rates for deleterious mutations,” he says.

That’s easier said than done. Lenski’s work has taken decades but there’s no reason why somebody with a bit of time on their hands might want to try González’ idea.

Another implication from this work is that background neutron radiation could be an important trigger for cancer in higher animals, such as humans. That makes sense but will need some looking into since there are other sources of spontaneous mutations that could also be responsible, such as the inhalation of radioactive elements like radon and who-knows-what other chemical processes that can disrupt DNA and its repair mechanisms.

Interesting work and another small step on the path to better understanding the origin of mutations in evolution.

Ref: arxiv.org/abs/1406.6641 : Mutagenesis and Background Neutron Radiation