The Complex Mathematics of Robot Wrestling
Here’s how mathematicians might define the sport of wrestling. A system composed of two mechanical agents coupled via mechanical actions such as contact and collision. The aim of the contest is for one agent to floor the other while maintaining its own balance. The rest is just show business.
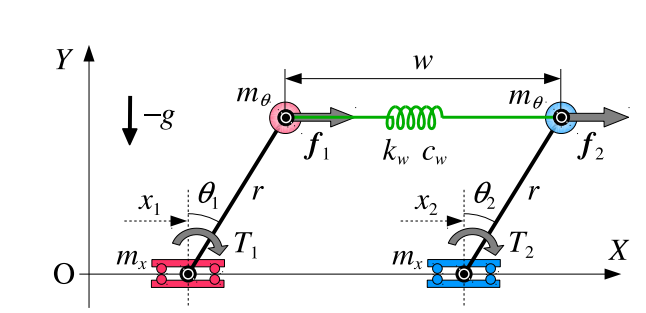
That’s more or less exactly how Katsutoshi Yoshida and pals at Utsunomiya University in Japan describe the sport in developing a mathematical model of wrestling which they go on to test in a numerical simulation.
The end result is a pair of autonomous mechanical wrestlers that compete to topple each other.
Their model is simple in principle. Each wrestler is an inverted pendulum on a cart that can move backwards and forwards, a bit like balancing a pencil on your finger.
These robot ‘wrestlers’ are joined at the tips by a spring that can stretch and compress. That means one wrestler can pull or push the other over.
However, the opposing wrestler can take evasive action by moving in a way that stabilises itself and unbalances its opponent. The contest is over when one wrestler or the other falls to the ground.
The question that Yoshida and co tackle is how best to design an intelligent controller that outperforms its opponent. The only action this controller can take is to move its cart backwards or forwards.
Although simple in principle, this problem turns out to be hugely complex. In creating a mathematical model of the contest, Yoshida and co identify 17 different parameters that influence the behaviour of the wrestlers. These include the mass and length of the pendulum, the mass of the cart, acceleration due to gravity, the various properties of the spring, friction and so on.
Each wrestler can end the bout in one of three configurations: standing up, having been pushed over or having been pulled over. So it’s not hard to see that there are nine possible outcomes in this contest.
Of these, five permutations correspond to a draw, with both wrestlers having been pushed or pulled to the ground or with both remaining upright. The other four permutations correspond to a win for one side or the other.
Each controller knows its own position and the position of its opponent. It also knows how its own movement will produce a turning force that tends to unbalance the inverted pendulum. The question that the controller must solve is how to move in a way that maintains the upright position of its own pendulum while exerting a turning force that unbalances the opponent.
To simplify matters, Yoshida and co assumed that the spring is more or less rigid. “Although human wrestling involves more flexible interactions between agents, this allows us substantially to reduce the computational efforts,” they say.
But to avoid the trivial situation in which one controller simply drags the other over using brute force, Yoshida and co limit the impulse that each can produce. This turns the context into something of a chess game.
One problem is that the solution space becomes so complex that the controllers cannot simulate it successfully and the contests end with the winner more or less chosen at random.
But Yoshida and co have an ingenious solution. It turns out that when one controller has a short delay built in to its calculations, it becomes about twice as successful as an opponent that does not have this delay.
That’s because undelayed controllers drive the system into complex states that they can no longer control but the delayed controllers never reach these levels of complexity and so turn out to be more successful.
So far, all of Yoshida and co’s work has been pure numerical simulation but they have ambitious plans. In future, they want to pitch their controllers against humans in a kind of human versus machine contest.
That surely will be no fair fight but it might be interesting to watch or even to take part in. WWE, watch out!
Ref: arxiv.org/abs/1405.7178 : Artificial Wrestling: A Dynamical Formulation of Autonomous Agents Fighting in a Coupled Inverted Pendula Framework
Keep Reading
Most Popular
Large language models can do jaw-dropping things. But nobody knows exactly why.
And that's a problem. Figuring it out is one of the biggest scientific puzzles of our time and a crucial step towards controlling more powerful future models.
How scientists traced a mysterious covid case back to six toilets
When wastewater surveillance turns into a hunt for a single infected individual, the ethics get tricky.
The problem with plug-in hybrids? Their drivers.
Plug-in hybrids are often sold as a transition to EVs, but new data from Europe shows we’re still underestimating the emissions they produce.
Stay connected
Get the latest updates from
MIT Technology Review
Discover special offers, top stories, upcoming events, and more.