One of the central puzzles of spacetime is its structure on the smallest scale.

The equations of general relativity are smooth, even at the tiniest scales. But in the early 1960s, the American physicist John Wheeler pointed out that in quantum mechanics, ordinary properties of spacetime, such as position, momentum and so on, have an uncertainty associated with them. That implies that spacetme must be uncertain as well. Wheeler famously described it as “quantum foam”.

Physicists would dearly love to study this foam but there’s a problem. Spacetime only becomes foam-like on the tiniest scale, at so-called Planck lengths of 10^-35 metres or so.

Probing that distance is obviously difficult. One way to do it is by accelerating particles to huge energies, which allows physicists to determine their position accurately, thereby probing very small volumes of space. 

But the energies required are around 10^19 GeV, many orders of magnitude higher than today’s particle accelerators. There’s no likelihood of reaching this energy on Earth in the foreseeable future so physicists are more or less resigned to the idea that they’ll never get their hands on quantum foam.   

They may change today thanks to a fascinating idea from Jacob Bekenstein, a physicist at the Hebrew University of Jerusalem in Israel. Bekenstein says he has worked out a way to measure the structure of spacetime on the Planck scale using a simple experiment involving little more than a block of glass and a laser. 

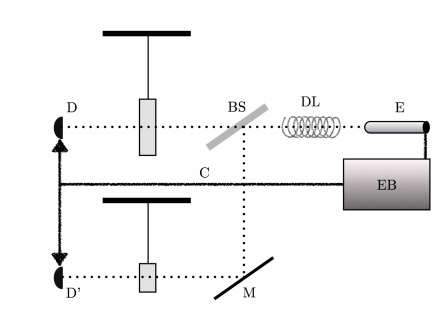
In essence, the experiment is straightforward.  Bekenstein’s goal is to move the block by a distance that is about equal to the Planck length. His method is simple: zap the block with a single photon.

The photon carries a small amount of moment and consequently pushes the block as it enters the glass, giving it some momentum.  As the photon leaves the block, the block comes to rest.

So the result of the photon’s passage is that it moves the block a small distance. 

Bekenstein’s idea is that if this distance is smaller than the Planck length, then the block cannot move and the photon cannot pass through it.  

So the experiment involves measuring the number of photons that pass through the block. If the number is fewer than predicted by classical optics, then that proves the existence of quantum foam.

In fact, by changing the momentum imparted by the photons, physicists ought to be able to measure the scale at which quantum foam effects kick in and perhaps quantify it other ways too.

The beauty of this experiment is that it avoids all the usual problems of probing small length scales using quantum particles which themselves experience uncertainty in their position.

Instead, Bekenstein’s experiment relies on conservation of momentum and the change in position of the centre of mass of a macroscopic block of glass. He shows that this does not violate of the uncertainty principle. Indeed, the only measurement involved is a straightforward photon count. 

Best of all, this experiment requires no device more exotic than a laser and a fridge (the block has to be cooled to close to zero to minimise thermal perturbations). Nothing about it is beyond the state of the art. Indeed, the test could be performed today on a tabletop in a well-equipped lab.

That’s not to say it will be easy. Bekenstein is a big cheese in the world of theoretical physics but colleagues will want to be sure that his argument is water tight before embarking on such an experiment.

If it is, then Bekenstein’s table top experiment could be up and running in the very near future offering the first potential glimpse of quantum foam.

Of course, the failure to find quantum foam would also be interesting. The latest thinking is that gravity is an emergent phenomenon through a kind of thermodynamic process. This does not require quantum foam.

So the failure to detect quantum foam, although not a proof of the emergent gravity theories, would certainly be a hugely interesting discovery too.

Either way, physicists could have some fun with this.  

Ref: arxiv.org/abs/1211.3816: Is A Tabletop Search For Planck Scale Signals Feasible?