Mathematics Reveals New Approach To The Perfect Putt

With a creak of the knees, you bend a fraction closer to the ball. You identify the gradient of the green, size up the distance to the hole and estimate the length and grade of the grass. Following a couple of finely judged practice swings, you’re ready to sink the perfectly judged putt.

That may be the time honoured way. But it turns out you’ve got it all wrong. According to Robert Grober, a physicist at Yale University in New Haven and a world expert on the science of golf, there’s a much better way to line up a putt.

Grober’s new insight comes from a simple mathematical analysis of the problem. To understand this insight, imagine a flat green with a small drop (ie at a small gradient to the horizontal. Now imagine a ball sitting a few feet from the hole on a line that is perpendicular to the fall.

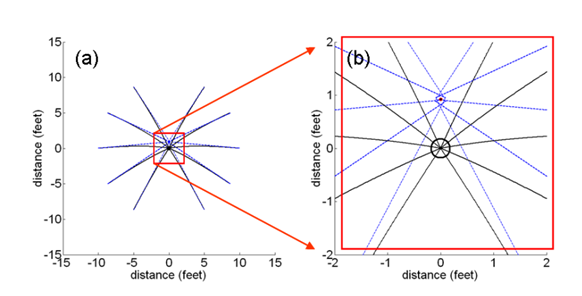
Obviously, the place to aim for is slightly above the hole, so that the fall steers the ball to its target. And that’s about as far as golfers have got with this problem. But Grober has gone further. He places other imaginary balls on an equidistant arc around the hole and then plots the targets to aim for for each one.

Now here’s the the surprise: it turns out that each of these targets lies within a small diamond-shaped area just above the hole. And for longer putts against steeper gradients, the smaller and further away from the whole this diamond becomes.

Grober says this insight can be put to immediate use: “While these computational results may seem esoteric, in fact they suggest a very simple technique for reading putts that can improve the probability of properly choosing the proper target line.”

Instead of determining a target line for a single putt, golfers should determine the target line for several equidistant putts along a 30 degree arc around the ball. The point (or small area) where these target lines coincide, is the place to aim for.

As Grober puts it: “By considering a family of putts all known to share the same target point, the golfer increases the probability of correctly identifying the target point, and thus the correct target line.”

Simple really. From now on, it’ll be impossible to miss.

Ref: arxiv.org/abs/1106.1698: The Geometry of Putting On a Planar Surface