The Power of Plant Clock Computing
One of the limitations of conventional thinking in computation is that computable functions proceed in a sequential manner, one independent step after another. When computer scientists talk of parallelism, they usually mean carrying out more than one of these independent linear computations at the same time.
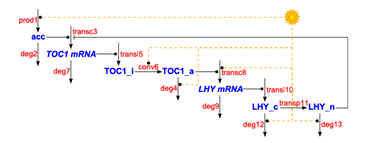
In the biological world, things are more complex because steps in biological computations may not be independent. Take, for example, the circadian rhythm in plants, the 24 hour cycle of biochemical processes that govern behaviour. The cycle has various important features such as the ability to synchronise with an external periodic light source and to continue to oscillate even in the absence of variations in illumination.
Biochemists have long known that these cycles are the result of various biochemical feedback loops in which the transcription of genes is boosted and damped.
Each feedback loop is part of a hugely complex biochemical network and is affected by many factors simultaneously, not least of which is the presence or absence of light and the state of the network with which it is most closely linked, which themselves may be interdependent feedback loops.
Of course, plant clocks have been studied for hundreds of years and a huge amount is known about how they work, particularly about Arabidopsis thaliana, a small flowering plant that is the standard object of study for plant biologists.
The trouble is that nobody has been able to accurately model the behaviour of these rhythms from first principles.
As luck would have it, just such a system has been waiting in the wings. Process algebra is a form of computation that can handle multiple simultaneous interdependent steps and this makes it perfect for modelling these tricky biochemical networks and the feedback loops that drive them.
The trouble is putting it into practice: process algebra is not an easy toy to play with.
Today, however, Ozgur Akman at the University of Edinburgh and a few pals outline how they’ve used this approach to model the circadian rhythm of the green alga Ostreococcus tauri, which has the honour of possessing the simplest planet clock yet discovered.
Akman and co created a model of the various feedback loops in the Ostreococcus clock using a process algebra known as Bio-PEPA. This allowed them to explore how the clock responds to factors such as changes in illumination patterns and to genetic mutations, a factor that effects how the clock might change over evolutionary time scales.
The team has even been able to use the model to make some predictions about the behaviour of the real Ostreococcus populations. “We predict that the qualitative behaviour of the free-running clock will be dependent on the size of the cellular population; while damped oscillations will be observed in large populations,” say Akman and co.
That’s interesting and important science and not just because these predictions should be straightforward to test or because of the important insights they give into plant biology.
The real importance is more subtle. An often overlooked property of process algebra is that it is not equivalent to a standard sequential Turing machine. Because process algebra encompasses concurrent processes and the communication between them, it is subtly different and potentially more powerful.
In exactly what ways isn’t yet clear, however. The study of process algebra is relatively recent. One important question asks what can be done with process algebra that cannot be done with a Turing machine. One answer may be related to the efficiency of calculations.
Several orders of magnitude separate the efficiency of biological computation from what is possible with silicon. If that difference turns out to be the result of process algebra, then the study and manipulation of networks such as the Ostreococcus clock, may turn out to be the trigger for a new generation of super-efficient computing.
Ref:arxiv.org/abs/1002.4661: Complementary Approaches To Understanding The Plant Circadian Clock
Keep Reading
Most Popular
Large language models can do jaw-dropping things. But nobody knows exactly why.
And that's a problem. Figuring it out is one of the biggest scientific puzzles of our time and a crucial step towards controlling more powerful future models.
The problem with plug-in hybrids? Their drivers.
Plug-in hybrids are often sold as a transition to EVs, but new data from Europe shows we’re still underestimating the emissions they produce.
Google DeepMind’s new generative model makes Super Mario–like games from scratch
Genie learns how to control games by watching hours and hours of video. It could help train next-gen robots too.
How scientists traced a mysterious covid case back to six toilets
When wastewater surveillance turns into a hunt for a single infected individual, the ethics get tricky.
Stay connected
Get the latest updates from
MIT Technology Review
Discover special offers, top stories, upcoming events, and more.